
Netzgespinste
Die Mathematik neuronaler Netze: einfache Mechanismen, komplexe Konstruktion
Neuronale Netze scheinen wie Menschen zu lernen, verstehen Sprache, Bilder und Strategiespiele. Ist das jetzt schon künstliche Intelligenz? Um das herauszufinden, hilft nur ein Blick in die Algorithmen. Und der lohnt sich, denn neuronale Netze sind wirklich schöne mathematische Gebilde.
Jahrzehntelang war mit neuronalen Netzen kein Blumentopf zu gewinnen, jetzt erobern sie die digitalisierte Welt im Sturm: Im Smartphone haben sie die Sprachverarbeitung übernommen, in der Bildersammlung die Gesichtserkennung und kürzlich wurde eine noch sicher geglaubte Bastion menschlicher Intelligenz gestürmt: Eine Kombination aus mehreren neuronalen Netzen und anderen Algorithmen hat einen Profispieler im asiatischen Strategiespiel Go geschlagen (siehe Artikel auf S. 148).
Neuronale Netze beweisen eindrucksvoll, dass sie vielfältige kognitive Aufgaben übernehmen können – und verdrängen oder ergänzen in immer mehr Bereichen die bislang gebräuchlichen Algorithmen, darunter auch andere maschinelle Lernverfahren wie etwa die in der Spracherkennung genutzten Hidden Markov oder Gaussian Mixture Models. Die meisten dieser Ansätze versuchten, das Problem durch möglichst exakte Beschreibung von Merkmalen zu lösen und natürliche Variationen statistisch abzufangen. Gesichtsdetektoren etwa bestanden aus Bildverarbeitungsfiltern, die helfen sollten, bestimmte Merkmale wie Augen, Nase oder Mund zu extrahieren. Diese Verfahren waren sehr fehleranfällig, weil nicht jede Variation explizit modelliert werden konnte – etwa Brillen, Hüte, durch Drehung verdeckte Merkmale, individuelle Handschrift et cetera.
Neuronale Netze hingegen sind zunächst nicht auf das Erkennen bestimmter Merkmale getrimmt, nicht mal zwingend auf ein bestimmtes Fachgebiet. Sie bestehen aus sehr einfachen, dafür aber extrem vielen miteinander vernetzten mathematischen Funktionen. Erst im Laufe des Trainings, nach Ansicht Tausender bis Millionen von Beispielen, lernen die Netze, was wichtig ist: das Essenzielle an einem Gesicht, einer Katze, einem Hund oder einem Flugzeug.
Mit jedem neuen Trainingsbeispiel erhält das Netz Feedback über seine Erkennungsleistung und justiert daraufhin seine unzähligen Parameter neu, sodass sich die einfachen Basisfunktionen im Laufe der Zeit zu genau den Verarbeitungsfiltern formen, die zum Lösen der Aufgabe wichtig sind. Die Netze lernen dabei mathematische Funktionen unterschiedlicher Komplexität, sie bauen sich ihr Handwerkszeug selbst: Trainiert man ein neuronales Netz mit gesprochener Sprache, wird es mathematische Funktionen bilden, die Phoneme unterscheiden und in Folgen von Phonemen sinnvolle Wörter und Sätze erkennen.
Speist man Bilder ein, wird das Netz Funktionen lernen, die Strukturen, Kanten, Farbmuster, aber auch komplexe Bestandteile wie Augen, Nase oder ganze Gesichtspartien herausfiltern. Dass dies funktioniert, liegt an einer besonderen Eigenschaft der Netze und ihrer Basisfunktionen: Man kann beweisen, dass sich mit solchen Netzen beliebige nichtlineare Funktion konstruieren lassen, siehe c’t-Link am Ende des Artikels.
Neuronen und Synapsen
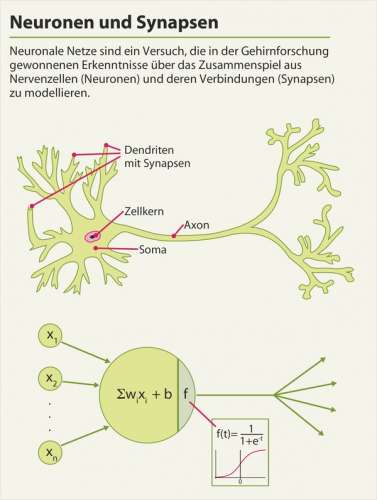
Neuronale Netze sind ein Versuch, die in der Gehirnforschung gewonnenen Erkenntnisse über das Zusammenspiel aus Nervenzellen (Neuronen) und deren Verbindungen (Synapsen) zu modellieren. Das menschliche Gehirn besitzt etwa 86 Milliarden Nervenzellen – also Zellen, die sich auf die Erregungsleitung und -übertragung spezialisiert haben. Jede Nervenzelle ist über Synapsen mit Hunderten bis Tausenden anderen Zellen verbunden, wobei es weder eine feste Verbindung noch für die Ewigkeit festgelegte Bedingungen für die Signalübertragung gibt. Die Zellen kommunizieren in der Regel über chemische Botenstoffe (Neurotransmitter), innerhalb des Neurons werden Signale elektrisch weitergeleitet.
Je näher eine Synapse am Soma – dem Zellkörper – ansetzt, desto stärker ist ihr Einfluss auf die Nervenzelle. Gleichzeitig ankommende Signale unterschiedlicher Nervenzellen addieren sich in ihrer Wirkung. Übersteigt der Reiz, den diese Botenstoffe in einem Neuron auslösen, eine bestimmte Schwelle, wird ein Aktionspotenzial ausgelöst; die Nervenzelle feuert.
Das Geflecht aus Neuronen und Synapsen nebst ihrer individuellen Reizschwellen ist nicht starr, sondern justiert sich immer wieder neu anhand der Erfahrungen und Eindrücke, die auf den Menschen von der Geburt bis ins Erwachsenenalter einströmen. Vor allem: Einzelne Neuronen oder kleinere Verbände entwickeln die Fähigkeit, sich auf das Erkennen komplexer Gebilde zu spezialisieren. So haben die Forscher in Versuchen mit Probanden festgestellt, dass beim Anblick eines Gesichts nur bestimmte Nervenzellen feuern.
Andere Neuronen reagieren auf spezifische Gesichtspartien oder -ausdrücke. Es scheint auch Neuronenverbände zu geben, die allgemein das Prinzip eines Gesichts verinnerlicht haben, und weitere, die auf individuelle Gesichter ansprechen, etwa von engen Freunden oder Familienmitgliedern.
Künstliche Netze: Stark vereinfacht
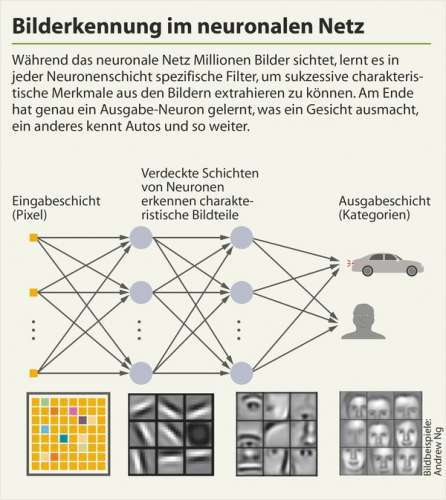
Ein künstliches neuronales Netz besteht aus drei Typen von Schichten: Die erste Neuronenschicht dient dazu, Roh- beziehungsweise leicht vorverarbeitete Informationen ins Netz einzuspeisen. Diese Eingabe-Neuronen kann man sich als diejenigen Signale vorstellen, die Sinnesorgane wie Haut, Retina oder Ohr aufnehmen.
Dazwischen liegen je nach Komplexität der Aufgabe ein bis zig Schichten mit verknüpften Neuronen. Diese sogenannten verdeckten Schichten lernen während des Trainings anhand Hunderttausender bis Millionen von Beispielen, aus den Rohinformationen zunächst simple Muster und Strukturen herauszulesen und aus diesen dann immer komplexere typische Merkmale zu formen, um die gestellte Aufgabe lösen zu können. Die letzte Schicht besteht aus Ausgabe-Neuronen, die sämtliche möglichen Ergebnisse repräsentieren.
Ein einfaches Beispiel: Geht es etwa darum, Ziffern in Bildern mit 28 × 28 Pixeln Kantenlänge zu erkennen, besteht die Eingabeschicht aus 784 Neuronen. Jedes dieser Neuronen repräsentiert ein Bildpixel – genauer dessen Helligkeitswert. Schwarze Pixel haben einen Helligkeitswert von 0 (Prozent), weiße 100 (Prozent), Graustufen liegen dazwischen.
Die Ausgabeschicht enthält für jedes mögliche Ergebnis ein Neuron, umfasst hier also zehn Neuronen, die die Ziffern von Null bis Neun repräsentieren. Bei der allgemeinen Objekterkennung wachsen sowohl Ausgabe- als auch Eingabeschicht auf Zig- bis Hunderttausende Neuronen: Die für das Training verwendete Standard-Sammlung ImageNet enthält im Schnitt Bilder mit einer Auflösung von 400 × 350 Pixeln, das ergibt bei Farbbildern 140 000 × 3 = 420 000 Eingabe-Neuronen. Theoretisch sind durchaus 100 000 unterschiedliche Objektkategorien, also Ausgabe-Neuronen, denkbar.
Im Gehirn beeinflussen nicht alle Neuronen einander gleich stark, unter anderem kommt es auf die Nähe der Synapse zum Soma an. Künstliche neuronale Netze bilden dies nach: Jede Verbindung zwischen zwei Neuronen besitzt dort ebenfalls ein individuelles Gewicht. Je höher das Gewicht, desto größer ist der Reiz, den das eine auf das andere ausübt.
Wie ein Neuron auf diesen kumulierten Reiz reagiert, kann man mathematisch auf mehrere Arten modellieren, am einfachsten mit einer Schwellenfunktion, die nur zwei Aktivitätslevel kennt: Übersteigt der Reiz den individuellen Schwellenwert des Neurons, gibt es den Wert 1 aus. Es wird aktiviert. Bleibt der Reiz darunter, gibt es den Wert 0 aus.
Lernen würde in einem solchen Netz bedeuten, die passenden Werte für die Gewichte zwischen den Kanten und die Schwellenwerte der Neuronen zu bestimmen. Diskrete Schwellenfunktionen haben allerdings den Nachteil, dass minimale Änderungen an den Gewichten das Ergebnis komplett zum Kippen bringen können – womit sich das Austarieren der Gewichte und Schwellenwerte nur schlecht realisieren lässt. Deshalb wählt man stetige Aktivierungsfunktionen, die den Übergang sanfter gestalten, etwa die Sigmoid-Funktion.
Dort gibt es keine sprunghafte Änderung des Aktivitätslevels – es liefert immer eine von der gewichteten Summe der Eingangssignale abhängige Ausgabe. Die Funktion simuliert die zwei Aktivitätslevel des diskreten Modells näherungsweise: In einem großen Bereich schwacher Eingangsreize erzeugt sie ebenfalls ein sehr niedriges, nah am Minimum liegendes Ausgangssignal. Ebenso liegt die Ausgabe für einen großen Bereich starker Inputs nah am Maximum. In einem relativ schmalen, mittleren Bereich der Eingangssignale steigt die Kurve relativ stark an. Der sogenannte Bias bestimmt dabei, wie stark der kumulierte Reiz sein muss, um das Neuron überhaupt anzuregen. Er verschiebt also das Grundniveau der Aktivierung. Man kann sich den Bias als Empfindlichkeit des Neurons vorstellen.
Jetzt könnte man sich auf die Suche nach den richtigen Bias und Gewichten machen – aber wie? Man könnte etwa sämtliche Parameter einfach so lange variieren, bis diejenige Kombination gefunden ist, die die meisten korrekten Treffer liefert – angesichts von Milliarden Verbindungen aber kein zielführender Ansatz.
In der Regel würden kleinere Gewichtsänderungen die Anzahl korrekt erkannter Beispiele nicht verändern, was es erheblich erschwert, eine effiziente Strategie für die Anpassung der Parameter zu entwickeln. Also ersetzt man das naheliegende Qualitätsmaß „Anzahl korrekter Treffer“ durch eines, das sich differenzierter verhält. Ein solches ist die quadratische Kostenfunktion. Diese Funktion berechnet die mittlere quadratische Abweichung, die das Netz bei Eingabe der Trainingsbilder produziert.
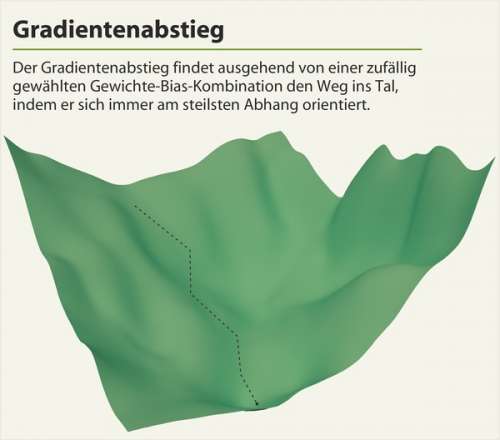
Ziel ist es, eine Gewichte-Bias-Kombination zu finden, die den geringsten Fehler produziert. Dafür gibt es eine Gradientenabstieg genannte Technik. Es ist ein Näherungsverfahren, eine exakte Berechnung wäre bei den Milliarden Gewichten der komplexen Netze unmöglich.
Man kann sich die Kostenfunktion im Dreidimensionalen vorstellen wie eine sehr abwechslungsreiche Landschaft aus steilen Bergen, tiefen Tälern, Hügeln, sanften Senken, Ebenen und Hochebenen. Das tiefste Tal dieser Funktion ist das globale Minimum, also genau diejenige Kombination von Gewichten und Bias, mit der das Netz die höchste Erkennungsquote (geringste Fehlerrate) liefert. In der Praxis hat diese Funktion gerne mal Millionen von Dimensionen – und genau das führt die Wissenschaftler und die Algorithmen wieder an die Grenzen des Machbaren. Der US-amerikanische Mathematiker Richard Bellman hat dafür den Begriff Curse of dimensionality, zu deutsch Fluch der Dimensionalität, geprägt.
Im Dreidimensionalen kann man sich die Strategie hinter dem Gradientenabstieg ungefähr so vorstellen: Es herrscht dichter Nebel, an irgendeinem Punkt in dieser Landschaft steht ein Mensch und soll den Weg ins Tal finden – möglichst schnell, bevor es dunkel wird. Er besitzt ein Gerät, mit dem er hin und wieder die Steigung messen kann, sollte dies aus Zeitgründen allerdings nicht zu oft tun.
Die beste Strategie ist in diesem Fall, an jedem Messpunkt die Richtung des steilsten Abstiegs einzuschlagen. Wählt er die Abstände zu groß, verpasst er vielleicht den optimalen Weg. Wählt er sie zu klein, bewegt er sich zu langsam fort. Diese Abstände kann man als Lernrate des Netzes interpretieren. Die Kunst ist, die Fehlerrate so zu wählen, dass man sich gleichzeitig schnell und zielgerichtet talwärts bewegt. So geht es schrittweise immer den steilsten Abhang hinab, bis eine Senke erreicht wird – das Minimum. Dieser Punkt ist eine Kombination aus Gewichten und Bias, die die Kostenfunktion und damit die Fehlerrate minimieren – zumindest für den zuvor gewählten Ausgangspunkt.
Um die Gradienten (also die lokalen Steigungen) zu bestimmen, wurde bereits in den 70er-Jahren ein zentrales Verfahren namens Backpropagation entwickelt, das aber erst 1986 von drei Forschern mathematisch so ausformuliert wurde, dass es in der Praxis erfolgreich eingesetzt werden konnte – einer davon Geoffrey Hinton, der später bei Google für den Durchbruch neuronaler Netze in der Bilderkennung sorgte.
Mit dem Backpropagation-Verfahren wird der am Ende errechnete Fehler Schicht für Schicht in das Netz zurückgespeist. In der Praxis bedeutet dies, dass der Fehler der Ausgabeschicht zunächst anteilig auf die Gewichte der letzten verdeckten Schicht verteilt wird, sodass man für jedes Neuron dieser Schicht eine individuelle Abweichung – in der Mathematik durch ein Delta symbolisiert – errechnen kann, die es anschließend wiederum anteilig an seine Vorgänger verteilt.
Dieses Verfahren geht so lange, bis jedes Gewicht im Netz bis hinab zur ersten Schicht einen solchen Delta-Wert erhalten hat. Erst dieses Fehler-Verteilungsverfahren ermöglicht es, die zahllosen Gewichte als direkte Stellschrauben zur Fehlerminimierung einzusetzen – durch Minimierung der Delta-Werte. Das Training eines neuronalen Netzes ist also ein iteratives Verfahren, in dem folgende Schritte so lange wiederholt werden, bis die Fehlerrate unter eine vorher festgelegte Schwelle sinkt:
1. Initialisierung des Netzes, etwa mit Zufallszahlen: Alle Gewichte und Bias tragen nun einen Wert zwischen Null und Eins.
2. Trainingsbeispiel x wird ins Netz eingespeist.
3. Feed-Forward-Schritt: Aus den Eingabewerten x können mithilfe der Gewichte die kumulierten Reize und dann mithilfe der Aktivierungsfunktionen und Bias die Ausgabe jedes Neurons Schicht für Schicht berechnet werden – bis hin zur Ausgabeschicht. Jedes Ausgabe-Neuron wird dann einen Wert zwischen Null und Eins tragen. Je höher dieser Wert, umso höher schätzt das Netz die Wahrscheinlichkeit, dass das Beispiel zu dieser Kategorie passt.
4. Berechnung des mittleren quadratischen Fehlers. Weil die Gewichte und Bias als Zufallszahlen initiiert werden, ist der Fehler im ersten Durchlauf normalerweise sehr hoch.
5. Backpropagation: Der in Schritt 4 errechnete Fehler wird wieder anteilig auf die Gewichte und Bias im Netz verteilt, und zwar zunächst von der Ausgabeschicht auf die letzte verdeckte Schicht, bis hinab zur Eingabeschicht. Ein Neuron mit hoher Abweichung vom Zielwert verteilt also auch höhere Abweichungs-Werte an seine Vorgänger.
6. Aktualisieren der Netzparameter (beziehungsweise deren Delta-Werte) unter Berücksichtigung der Lernrate.
7. Neuer Durchlauf (Feed-Forward plus Backpropagation) mit neuem Trainingsbeispiel, aktualisierten Gewichten und Bias.
Tiefe und Vielfalt
Es gibt bislang noch keine universelle Netzarchitektur (vergleichbar mit dem Nervensystem des Menschen), die den vielfältigen kognitiven Aufgaben rund um Erkennung, Verarbeitung und Problemlösung gewachsen ist. Vielmehr arbeiten die Forscher mit unterschiedlichen, an die jeweiligen Anforderungen angepassten Varianten.
Eines haben sie gemeinsam: Je komplexer die Aufgabe, umso tiefer müssen die Netze sein, kurz: Je mehr Schichten, desto besser. Dafür hat sich der Begriff Deep Learning etabliert. Die zusätzlichen Schichten gewinnbringend einzusetzen ist eine der großen Herausforderungen in der KI-Forschung. Obwohl man noch keine exakte Vorstellung davon hat, was genau innerhalb der riesigen Netze abläuft, müssen die Wissenschaftler ein Gefühl für potenzielle Verbesserungen entwickeln und eine passende Netzarchitektur austüfteln. Einen Durchbruch erzielte vor einigen Monaten Microsoft Research Asia (MRSA), das mit seinem 152-lagigen Netzwerk für die Bilderkennung den wichtigen ILSVRC-Wettbewerb (ImageNet Large Scale Visual Recognition Challenge) in mehreren Disziplinen gewann.
Aufgrund ihrer Architektur unterscheidet man vorwärtsgerichtete (Feed Forward, FFN), Rekurrente (RNN) und Long Short Term Memory Netze (LSTM). Erstere verknüpfen die Neuronen strikt von der Eingabe- hin zur Ausgabeschicht, RNNs können auch Neuronen mit sich selbst oder mit Neuronen aus tieferen Schichten verknüpfen und LSTMs sind gewissermaßen praxistaugliche RNNs, siehe unten.
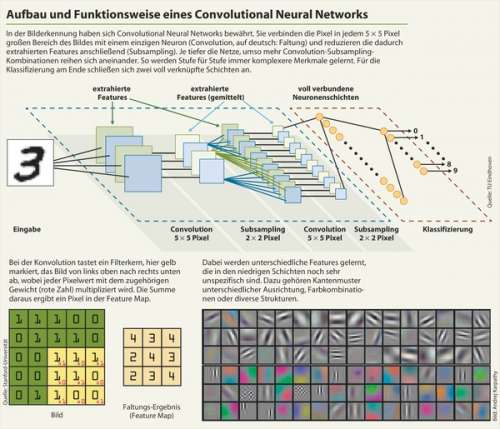
In der Bilderkennung haben sich die vorwärtsgerichteten Deep Convolutional Neural Networks (Deep CNNs) durchgesetzt, weil sich durch deren speziellen Aufbau schon einiges Vorwissen modellieren lässt. Für die Bilderkennung ist es nicht optimal, jedes Eingabe-Neuron (Pixelwert) mit jedem Neuron der ersten verdeckten Schicht zu verbinden. Damit würde man der Beziehung zwischen weit auseinanderliegenden Pixeln dieselbe Bedeutung verleihen wie benachbarten, was der räumlichen Struktur von Bildern nicht gerecht würde.
Deshalb konstruiert man das Netz so, dass es das Bild in kleinen Ausschnitten abtastet, etwa einer Region von 5 × 5 Pixeln, wobei jedes darin enthaltene Pixel mit einem Neuron verknüpft wird. Diese Region nennt man Local Receptive Field. Dieses Feld lässt man ein Pixel weiterwandern, verknüpft dessen Inhalt mit dem zweiten Neuron und so weiter. Die Gewichte an den Synapsen bleiben dabei gleich. Durch die unterschiedlich starke Aktivierung der Neuronen entsteht für jede besuchte Region ein Pixel auf der nächsten Ebene. Auf diese Weise baut sich ein Bild auf, das einer weiteren Schicht als Eingabe dient. Das entstandene Muster hat zunächst die gleiche Auflösung wie das Ursprungsbild. Interessant ist aber nur, ob das Muster in einem Bereich vorkommt, sodass die Auflösung vor der nächsten Schicht reduziert werden kann. Bei der Zusammenfassung benachbarter Bildbereiche interessiert üblicherweise nur das Neuron, das am stärksten feuert.
Was diese spezielle Art der Verknüpfung bewirken soll, wird klarer, wenn man dem Begriff Convolution (Faltung) auf den Grund geht. Faltungsfunktionen sind gängige Bildbearbeitungsfilter wie etwa Schärfen, Weichzeichnen, Glätten oder Kanten betonen. All diese Filter können als quadratische 3 × 3- oder 5 × 5-Matrix definiert werden, deren Gewichte sich natürlich unterscheiden. Der jeweilige Effekt entsteht, indem die Bildpixel bereichsweise mit den Werten der Faltungsmatrix multipliziert und aufsummiert werden. Übertragen auf das neuronale Netz bedeutet dies: Die spezielle Art der Abtastung und Verknüpfung bewirkt, dass das Netz Faltungsfunktionen unterschiedlicher Art lernt. Nach mehreren Convolution-Subsampling-Schritten hat das Netz zahllose Basisstrukturen und -Texturen extrahiert. Am Ende kombinieren voll verknüpfte Neuronenschichten die höherwertigen Merkmale – etwa Augen, Münder oder Nasen – zu einer Klassifizierung in der letzten Schicht.
Am besten kann man sich das Verfahren vorstellen, indem man selbst ein wenig herumexperimentiert: Über die Photoshop-Funktion „Eigene Filter“ oder die Gimp-Funktion „Faltungsmatrix“ können Sie selbst Filterkerne definieren und auf Bilder anwenden, Werte für die gängigen Filter finden Sie auf gimp.org. Eine schöne Echtzeit-Berechnung mit Beispielwerten hat die Stanford-Universität online gestellt, und im Blog des KI-Experten Andrej Karpathy kann man einem neuronalen Netz bei der Arbeit zuschauen, Quellen siehe c’t-Link.
CNNs lassen sich auch wesentlich effizienter verarbeiten: Es müssen deutlich weniger Gewichte gespeichert werden und die Berechnungen lassen sich hervorragend auf der GPU parallelisieren. Die immer leistungsfähigeren GPUs bilden daher das Fundament für die Erfolgsgeschichte der neuronalen Netze.
Rekurrente Neuronale Netze (RNN) verarbeiten die Eingabe nicht nur von Schicht zu Schicht, sondern leiten Reize auch von höheren in niedrigere Schichten – oder zu sich selbst – zurück. Das kann man sich so vorstellen wie eine Art extremes Kurzzeitgedächtnis, was das Netz dazu befähigt, Abfolgen von Eingaben zu verarbeiten, wie sie etwa in der Sprach- und Schreibschrifterkennung, beim Verfassen von Bildbeschreibungen oder der Interpretation von Videos benötigt werden.
Gesprochene Sätze etwa bestehen aus einer Abfolge von Lauten, die sich häufig erst im Kontext sinnvoll interpretieren lassen. Der Sinn einer Videosequenz mitten im Film erschließt sich nur, wenn man die Vorgeschichte kennt. Und aus mehreren Objekten im Bild lässt sich nur im Zusammenhang eine sinnvolle Beschreibung formen. Ein rekurrentes Netz erlaubt es, in tieferen Schichten gewonnene Erkenntnisse wieder vorne einzuspeisen. In der Praxis sind diese normalen RNNs aber nicht in der Lage, zu weit zurückliegende Informationen zu verknüpfen, etwa wenn sie in einem Text durch mehrere Absätze voneinander getrennt sind.
Diesen Nachteil haben die KI-Pioniere Sepp Hochreiter und Jürgen Schmidhuber bereits 1991 theoretisch nachgewiesen und sechs Jahre später das erste Netz mit Long Short Term Memory (LSTM) vorgestellt – einer der Meilensteine in der Entwicklungsgeschichte neuronaler Netze. LSTMs sind so konstruiert, dass sie sich Informationen über einen größeren Zeitraum merken können.
Dieses Gedächtnis befähigt sie beispielsweise dazu, längere Texte zu übersetzen oder zu interpretieren. Schmidhuber ist mittlerweile Leiter am Schweizer Forschungzentrum IDSIA. Hier haben übrigens auch einige Entwickler der Firma DeepMind ihre Wurzeln, die später von Google übernommen wurde und dieser Tage mit dem eingangs erwähnten Go-Computer AlphaGo einen Coup landete.
DeepMind-Gründer Demis Hasabis gehört zur jungen Generation der KI-Forscher und hat eine extrem interessante Biografie vorzuweisen: Seine erste Karriere machte er als Spieleentwickler, seine zweite als Neurowissenschaftler – bis er schließlich als KI-Unternehmensgründer beide Bereiche zusammenbrachte.
DeepMind entwickelt sogenannte Reinforcement-Systeme (verstärkendes Lernen), die allein anhand der Betrachtung von Spielzügen sowohl die Regeln lernen als auch erfolgreiche Gewinnstrategien entwickeln. Das Aufregende: Während die Sprach- und Bilderkennungssysteme überwachtes Lernen praktizieren (jede Eingabe gehört zu exakt einer Ausgabekategorie), ist verstärkendes Lernen bereits eine Mischform aus überwachtem und unüberwachtem Lernen. Dessen Vorbild ist ein fein abgestimmtes Belohnungssystem, wie es auch den Menschen zu Handlungen motivieren soll.
Zukunft
Neuronale Netze faszinieren. Ihre Stärke spielen sie vor allem in Bereichen aus, in denen es darum geht, riesige Mengen an Fakten oder Messwerten zu bewerten: Kein Mensch kann annähernd so viele Daten aus seinem Gedächtnis abrufen wie ein Computer aus den Datenspeichern dieser Welt. Doch bei aller Begeisterung sollte man man die Netze nicht als Universalwerkzeug für alle Lebenslagen missverstehen. Andere maschinelle Lernverfahren wie die Support Vector Machine eignen sich für Alltagsaufgaben häufig besser, weil sie leichter zu kontrollieren sind, siehe Artikel auf Seite 137.
Auch das menschliche Gehirn beziehungsweise die menschliche Intelligenz bleibt vorerst überlegen. Künstliche neuronale Netze sind noch nicht geeignet, größere Transferleistungen zu erbringen, also mit ihrem erlernten Wissen beliebige Situationen zu meistern oder selbst kreativ zu werden, etwa spielerisch mit Sprache umzugehen. Oder, bezogen auf sich selbst: Sie können noch nicht mal ihre eigenen Unzulänglichkeiten erkennen.
Zur Analyse und Optimierung der Netze benötigt man nach wie vor menschlichen Erfindergeist oder so etwas wie ein Gespür für erfolgversprechende Ansätze. Und letztlich sind die Netze noch weit von einem Generalisten entfernt, der sich zu einem Individuum mit eigenen Interessen entwickelt.
Wissenschaftler wie Yann LeCun oder Jürgen Schmidhuber sehen die Zukunft daher in unüberwachten Techniken – also in Systemen, die sich selbstständig auf Lernenswertes fokussieren und allein durch Beobachtung Zusammenhänge erkennen. In dieser Disziplin lässt ein echter Durchbruch noch auf sich warten. (atr@ct.de)
Literatur, Tutorials, Online-Netzsimulationen: ct.de/ypt8
