Missing Link: Stephen Wolfram über die Rolle der KI in der Forschung (Teil 1)

Inhaltsverzeichnis

Dieser Beitrag wurde uns mit freundlicher Genehmigung von Stephen Wolfram zur Verfügung gestellt: Stephen Wolfram (2024), "Can AI Solve Science?", Stephen Wolfram Writings.

Vor allem angesichts der jüngsten Überraschungserfolge ist der Glaube weitverbreitet, dass die Künstliche Intelligenz eines Tages "alles" kann – oder zumindest alles, was wir derzeit tun. Und was ist mit der Wissenschaft? Im Laufe der Jahrhunderte haben wir Menschen schrittweise Fortschritte gemacht und allmählich das aufgebaut, was heute im Wesentlichen das größte intellektuelle Gebäude unserer Zivilisation ist. Aber trotz all unserer Bemühungen gibt es immer noch alle möglichen wissenschaftlichen Fragen, die offen sind. Kann die künstliche Intelligenz nun kommen und sie einfach alle lösen?

Bei der Frage, ob KI die Wissenschaft vollständig lösen kann, lautet die Antwort zwangsläufig und deutlich Nein. Das bedeutet jedoch nicht, dass KI keinen bedeutenden Beitrag zur wissenschaftlichen Entwicklung leisten kann. Large Language Models (LLMs) bieten beispielsweise eine innovative sprachliche Schnittstelle zu Computertechnologien, wie sie auch in der Wolfram Language implementiert sind. LLMs haben aufgrund ihres Verständnisses des etablierten wissenschaftlichen Wissens das Potenzial, auf höchstem Niveau wie eine intelligente Autovervollständigung zu arbeiten, die konventionelle Antworten oder die nächsten Schritte in wissenschaftlichen Prozessen vorschlägt.

Ich möchte hier jedoch auf tiefer gehende Fragen der KI in der Wissenschaft eingehen. Vor drei Jahrhunderten hat die Idee, die Welt mit Hilfe der Mathematik darzustellen, die Wissenschaft verändert. Und heute befinden wir uns inmitten eines großen Wandels hin zu einer grundlegend computergestützten Darstellung der Welt (und ja, genau darum geht es bei unserer Computersprache Wolfram Language). Wie steht es also um die KI? Sollten wir sie im Wesentlichen als ein praktisches Werkzeug betrachten, das den Zugang zu bestehenden Methoden ermöglicht, oder bietet sie der Wissenschaft etwas grundlegend Neues?

Über Stephen Wolfram

Stephen Wolfram ist ein britischer Physiker, Mathematiker und Unternehmer, bekannt für die Entwicklung der Wolfram Language und Mathematica, sowie für sein Buch "A New Kind of Science".

Was kann man von KI in der Wissenschaft erwarten

Ich möchte erforschen, was KI in der Wissenschaft leisten kann und was nicht. Dafür schaue ich mir spezifische, vereinfachte Beispiele an, um die Kernpunkte deutlich zu machen. Ich werde meine Gedanken und Erwartungen teilen, die auf unseren bisherigen Beobachtungen basieren. Zudem diskutiere ich einige theoretische und philosophische Aspekte darüber, was machbar ist und was nicht.

Was verstehen wir eigentlich unter KI? In der Vergangenheit wurde alles, was ernsthaft mit Computern zu tun hat, oft als Künstliche Intelligenz betrachtet. In diesem Fall würde insbesondere das, was wir seit Langem mit unserer Computersprache Wolfram Language machen, als KI gelten – ebenso wie all meine Studien über einfache Programme im Computeruniversum. Aber hier werde ich meistens eine engere Definition verwenden und sagen, dass KI etwas ist, das auf maschinellem Lernen basiert (und normalerweise mit neuronalen Netzen implementiert wird), das schrittweise anhand von Beispielen trainiert wird, die ihm gegeben werden.Zusätzlich berücksichtige ich oft, dass die Trainingsbeispiele entweder eine große Menge menschlicher wissenschaftlicher Texte oder reale Weltbeobachtungen enthalten. Das bedeutet, die KI lernt nicht nur roh, sondern auch aus einer breiten Palette von Wissen, das auf menschlichen Erkenntnissen basiert.

"Missing Link"

Was fehlt: In der rapiden Technikwelt häufig die Zeit, die vielen News und Hintergründe neu zu sortieren. Am Wochenende wollen wir sie uns nehmen, die Seitenwege abseits des Aktuellen verfolgen, andere Blickwinkel probieren und Zwischentöne hörbar machen.

• Mehr zum Feuilleton "Missing Link"

Jetzt haben wir eine gemeinsame Definition von KI. Aber was bedeutet nun Wissenschaft und was bedeutet es, Wissenschaft zu betreiben? Im Kern geht es darum, Phänomene, die "da draußen in der Welt" existieren (meist in der natürlichen Welt), zu erfassen oder in Konzepte zu übersetzen, über die nachgedacht oder die durchdacht werden können. Die eigentliche wissenschaftliche Arbeit folgt jedoch mehreren, recht unterschiedlichen und weitverbreiteten "Arbeitsabläufen". Einige befassen sich mit Vorhersagen: Ausgehend von beobachtetem Verhalten sollen zukünftige Ereignisse vorhergesagt werden; es wird ein Modell gesucht, das klar beschreibt, wie sich ein System verhalten wird; aus einer bestehenden Theorie sollen konkrete Implikationen abgeleitet werden. Andere Arbeitsprozesse konzentrieren sich auf Erklärungen: Ein Verhalten wird in eine für Menschen verständliche Erklärung überführt; Analogien zwischen verschiedenen Systemen oder Modellen werden gesucht. Wieder andere Arbeitsabläufe konzentrieren sich auf die Erzeugung von Neuem: die Entdeckung von etwas, das bestimmte Eigenschaften hat; die Entdeckung von etwas "Interessantem".

Im Folgenden werde ich diese Arbeitsabläufe genauer untersuchen und zeigen, wie sie durch KI verändert werden können (oder auch nicht). Doch bevor ich damit beginne, möchte ich etwas erörtern, das jeden Versuch, "die Wissenschaft zu lösen", überschattet: das Phänomen der rechnerischen Irreduzibilität.

Die Grenze der rechnerischen Irreduzibilität

In der Wissenschaft ist es oft eine große Herausforderung, die zugrunde liegenden Regeln zu finden, nach denen ein System funktioniert. Aber nehmen wir an, wir haben diese Regeln gefunden, und wir haben eine formale Möglichkeit, sie darzustellen, beispielsweise als Programm. Dann stellt sich immer noch die Frage, was diese Regeln für das tatsächliche Verhalten des Systems bedeuten. Ja, wir können die Regeln explizit Schritt für Schritt anwenden und verfolgen, was passiert. Aber können wir auf einen Schlag einfach "alles lösen" und wissen, wie sich das System verhalten wird?

Dazu müssten wir in gewissem Sinne "unendlich viel schlauer" sein als das System. Das System muss all diese Schritte durchlaufen, aber irgendwie können wir "vorausspringen" und das Ergebnis sofort herausfinden. Ein Schlüsselgedanke – der letztlich durch das Wolfram-Physikprojekt unterstützt wird - besteht darin, dass wir uns alles, was geschieht, als einen Rechenprozess vorstellen können. Das System führt eine Berechnung durch, um sein Verhalten zu bestimmen. Wir Menschen – oder, was das betrifft, jede von uns geschaffene KI – müssen ebenfalls Berechnungen durchführen, um zu versuchen, dieses Verhalten vorherzusagen oder zu "lösen". Der Grundsatz der Gleichwertigkeit von Berechnungen besagt jedoch, dass diese Berechnungen in ihrer Ausgereiftheit höchstens gleichwertig sind. Das bedeutet, dass wir nicht erwarten können, das System systematisch "vorhersagen" oder "lösen" zu können; es erfordert unweigerlich einen gewissen, nicht reduzierbaren Rechenaufwand, um herauszufinden, was genau das System tun wird. So sehr wir uns auch bemühen, ob mit KI oder auf andere Weise, unsere "wissenschaftliche Leistung" wird letztlich durch die rechnerische Irreduzibilität (unzerlegbare Darstellung) des Verhaltens begrenzt sein.

Die Möglichkeit und Unmöglichkeit von Wissenschaft

Aber warum ist Wissenschaft trotz der rechnerischen Irreduzibilität überhaupt möglich? Der entscheidende Punkt ist, dass es immer bestimmte Aspekte eines Systems gibt, über die sich mit begrenztem rechnerischen Aufwand Aussagen treffen lassen, selbst wenn das Gesamtsystem rechnerisch irreduzibel ist. Diese erkennbaren und berechenbaren Eigenschaften sind es, auf die wir uns in der Wissenschaft üblicherweise konzentrieren.

Dabei gibt es jedoch unweigerlich Grenzen – und Probleme, die in die Irreduzibilität von Berechnungen münden. Manchmal zeigen sich diese als Fragen, die wir einfach nicht beantworten können, und manchmal als "Überraschungen", die wir nicht kommen sehen. Aber der Punkt ist, dass wir, wenn wir "alles lösen" wollen, unweigerlich mit der rechnerischen Irreduzibilität konfrontiert werden, und es wird einfach keine Möglichkeit geben – weder mit KI noch auf andere Weise –, das System Schritt für Schritt zu simulieren. Es gibt hier jedoch eine Besonderheit. Was ist, wenn wir nur Dinge wissen wollen, die mit der rechnerischen Irreduzibilität übereinstimmen? Ein großer Teil der Wissenschaft – und der Technologie – wurde speziell für rechnerisch reduzierbare Phänomene entwickelt. Das ist unter anderem der Grund, warum mathematische Formeln in der Wissenschaft so erfolgreich sein konnten, wie sie es sind.

Aber wir wissen natürlich, dass wir bisher nicht alles gelöst haben, was wir in der Wissenschaft wollen. Und in vielen Fällen scheint es so, als hätten wir keine wirkliche Wahl, was wir erforschen wollen; die Natur zum Beispiel zwingt es uns auf. Und das Ergebnis ist, dass wir unweigerlich mit der rechnerischen Irreduzibilität konfrontiert werden.

Wie ich noch erläutern werde, bietet KI Möglichkeiten, bestimmte Formen der rechnerischen Irreduzibilität aufzudecken und uns rationalisierte Ansätze zur Erforschung zu liefern. Dennoch wird es immer Aspekte geben, die aufgrund ihrer rechnerischen Komplexität zu unvorhergesehenen Überraschungen führen, die wir nicht einfach oder direkt verstehen können. Dieser Zustand wird sich nicht ändern. Ständig gibt es mehr zu entdecken, mehr zu berechnen, und neue Ebenen der Komplexität, von denen wir bisher nichts wussten. Letztendlich – mit oder ohne KI – stellt die rechnerische Irreduzibilität eine Grenze dar, die uns daran hindert, die Wissenschaft in ihrer Gänze vollständig zu "lösen".

Das alles hat einen merkwürdigen historischen Hintergrund. Zu Beginn des zwanzigsten Jahrhunderts stellte sich die Frage, ob die gesamte Mathematik "mechanisch gelöst" werden kann. Mit der Veröffentlichung des Gödelschen Unvollständigkeitstheorems schien das Gegenteil bewiesen. Und jetzt, da wir wissen, dass auch die Wissenschaft letztlich eine rechnerische Struktur hat, zeigt das Phänomen der rechnerischen Irreduzibilität – im Grunde eine Verschärfung des Gödelschen Theorems –, dass auch sie nicht "mechanisch gelöst" werden kann.

Wir können jedoch immer noch die Frage stellen, ob die Mathematik – oder die Wissenschaft –, die die Menschen studieren wollen, es schaffen könnte, nur in Taschen der rechnerischen Irreduzibilität zu leben. Aber in gewissem Sinne ist der eigentliche Grund dafür, dass "Mathematik schwer ist", der, dass wir ständig Beweise für die rechnerische Irreduzibilität sehen: Wir kommen nicht darum herum, Dinge tatsächlich berechnen zu müssen. Das ist zum Beispiel nicht das, was Methoden wie die KI mit neuronalen Netzen (zumindest ohne die Hilfe von Tools wie Wolfram Language) können.

Dinge, die in der Vergangenheit funktioniert haben

Bevor man sich mit den Einzelheiten dessen befasst, was moderne, auf maschinellem Lernen basierende KI bei der "Lösung wissenschaftlicher Probleme" leisten könnte, scheint es lohnenswert, sich daran zu erinnern, was in der Vergangenheit funktioniert hat – nicht zuletzt als eine Art Grundlinie für das, was moderne KI jetzt ergänzen könnte.

Ich selbst setze seit mehr als vier Jahrzehnten Computer und Berechnungen ein, um Dinge in der Wissenschaft zu entdecken. Mein erster großer Erfolg stellte sich 1981 ein, als ich beschloss, alle möglichen Regeln einer bestimmten Art (elementare zelluläre Automaten) aufzuzählen und sie dann auf einem Computer auszuführen, um zu sehen, was sie bewirken:

Ich war davon ausgegangen, dass bei einfachen zugrundeliegenden Regeln auch das endgültige Verhalten entsprechend einfach sein würde. Aber in gewisser Weise ging der Computer nicht davon aus: Er zählte einfach die Regeln auf und berechnete die Ergebnisse. Und so konnte er, obwohl ich es mir nie vorgestellt hatte, so etwas wie "Regel 30" entdecken.

Ich haben immer wieder ähnliche Erfahrungen gemacht: Ich kann nicht erkennen, wie ein System etwas "Interessantes" tun kann. Aber wenn ich systematisch die Möglichkeiten aufzähle, ist es da: etwas Unerwartetes, Interessantes und "Kluges", das der Computer tatsächlich entdeckt hat. Anfang der 1990er-Jahre habe ich mich gefragt, was die einfachste mögliche universelle Turing-Maschine sein könnte. Ich selbst wäre nie in der Lage gewesen, es herauszufinden. Die Maschine, die den Rekord seit den frühen 1960er-Jahren hielt, hatte sieben Zustände und vier Farben. Aber der Computer ließ mich durch systematische Aufzählung die Maschine mit zwei Zuständen und drei Farben entdecken, die 2007 als universell bewiesen wurde (und ja, es ist die einfachste universelle Turing-Maschine).

Im Jahr 2000 interessierte ich mich dafür, wie das einfachste mögliche Axiomensystem für die Logik (Boolesche Algebra) aussehen könnte. Das einfachste bis dahin bekannte System umfasste neun binäre (Nand-)Operationen. Durch systematisches Aufzählen von Möglichkeiten fand ich schließlich ein einziges Axiom mit sechs Operationen ((p · q) · r) · (p · ((p· r) · p)) = r (dessen Richtigkeit durch einen automatisierten Theorembeweis bestätigte). Noch einmal: Ich hatte keine Ahnung, dass es dieses Axiom gab, und ich wäre sicherlich nie in der Lage gewesen, es selbst zu konstruieren. Aber allein durch systematische Aufzählung war der Computer in der Lage, ein Ergebnis zu finden, das mir sehr "kreativ" erschien.

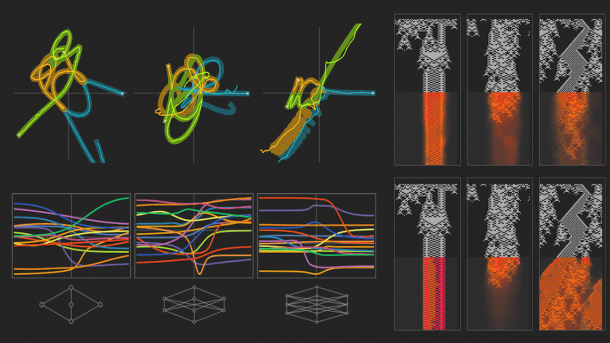
Im Jahr 2019 führte ich eine weitere systematische Aufzählung durch, dieses Mal von möglichen Hypergraphen-Umschreibregeln, die der niedrigsten Struktur unseres physikalischen Universums entsprechen könnten. Als ich mir die erzeugten Geometrien ansah, hatte ich das Gefühl, dass ich als Mensch das, was ich sah, grob einordnen konnte. Aber gab es Ausreißer? Ich wandte mich an etwas, das der "modernen KI" näher stand, um die Wissenschaft zu betreiben - die Erstellung einer Merkmalsraumdarstellung visueller Aufnahmen:

Es brauchte mich als Menschen, um es zu interpretieren. Aber ja, es gab Ausreißer. Diese waren praktisch "automatisch entdeckt" worden vom neuronalen Netz, das das Merkmalsraumdiagramm erstellte.

Ich möchte noch ein weiteres Beispiel aus meiner persönlichen Erfahrung anführen, ein Beispiel ganz anderer Art. Damals, im Jahr 1987, waren wir Teil der Entwicklung von Version 1.0 der heutigen Wolfram Language. Unser Ziel war es, Algorithmen zu entwickeln, um Hunderte von mathematischen Spezialfunktionen über einen riesigen Bereich von Argumenten zu berechnen. Früher hatte man mühsam Reihenapproximationen für bestimmte Fälle berechnet. Unser Ansatz war jedoch anders.

Wir entschieden uns für eine Art maschinelles Lernen und investierten monatelang Computerzeit, um Parameter an rationale Näherungen anzupassen. Heutzutage könnten wir etwas Ähnliches mit neuronalen Netzen anstelle von rationalen Näherungen machen. Aber in beiden Fällen zielt das Konzept darauf ab, ein allgemeines Modell der "Welt", mit der man es zu tun hat (in diesem Fall die Werte spezieller Funktionen), zu finden. Dann versucht man, die Parameter des Modells anhand tatsächlicher Daten zu lernen. Dies ist nicht gerade "lösende Wissenschaft", und es erlaubt einem nicht, "das Unerwartete zu entdecken". Es ist jedoch ein Bereich, in dem "KI-ähnliches" Wissen über allgemeine Erwartungen bezüglich der Glattheit oder Einfachheit es ermöglicht, das Analogon eines wissenschaftlichen Modells zu konstruieren.

Das ist nicht die einzige Aufgabe der Wissenschaft. Die folgenden Abschnitte widmen sich weiteren Aspekten. Was jedoch oft als Kennzeichen erfolgreicher wissenschaftlicher Arbeit galt, ist ihre Vorhersagekraft: Kann vorhergesagt werden, was geschehen wird? Es stellt sich somit die Frage, ob KI dramatisch verbesserte Möglichkeiten für solche Vorhersagen bietet.

Kann KI vorhersagen, was passieren wird?

Im einfachsten Fall soll KI genutzt werden, um induktive Schlussfolgerungen zu ziehen. Man gibt die Ergebnisse einer Reihe von Messungen ein und bittet dann die KI, die Ergebnisse von Messungen vorherzusagen, die bisher nicht durchgeführt wurden. Auf dieser Ebene wird die KI wie eine Blackbox behandelt; es spielt keine Rolle, was im Inneren passiert; es interessiert nur, ob die KI die richtige Antwort gibt. Man könnte denken, dass es möglich ist, die KI irgendwie so einzurichten, dass sie "keine Annahmen trifft" und nur "den Daten folgt". Aber es ist unvermeidlich, dass der KI eine Struktur zugrunde liegt, die sie letztlich dazu bringt, eine Art Modell für die Daten anzunehmen.

Ja, dieses Modell kann sehr flexibel sein. Aber ein wirklich "modellloses Modell" kann es nicht geben. Vielleicht basiert die KI auf einem riesigen neuronalen Netz mit Milliarden von numerischen Parametern, die verändert werden können. Vielleicht kann sich sogar die Architektur des Netzes ändern. Aber der gesamte Aufbau des neuronalen Netzes definiert unweigerlich ein ultimatives zugrunde liegendes Modell.

Betrachten wir einen sehr einfachen Fall. Stellen wir uns vor, dass unsere "Daten" die blaue Kurve im folgenden Bild sind – die vielleicht die Bewegung eines an einer Feder aufgehängten Gewichts darstellt. Die Physik sagt dann die rote Kurve voraus. Nimmt man nun ein sehr einfaches neuronales Netz und trainiert es mit den obigen Daten der "blauen Kurve", um ein Netz mit einer bestimmten Sammlung von Gewichten zu erhalten.

Das Resultat sieht dann wie folgt aus:

Man sieht, dass das Netz die Daten, auf denen es trainiert wurde, gut reproduziert, aber wenn es um die "Vorhersage der Zukunft" geht, versagt es grundsätzlich. Was ist hier also los? Haben wir einfach nicht lange genug trainiert? Das ist nicht das Problem. Denn egal, ob man mehr Runden trainiert, größere neuronale Netze oder andere Aktivierungsfunktionen (für das neuronale Netz) verwendet, das Problem bleibt.

Die Idee, eine Funktion durch eine Kombination von Standardfunktionen zu approximieren, ist natürlich sehr alt (man denke an die Epizyklen und früher). Neuronale Netze ermöglichen es, kompliziertere (und hierarchische) Kombinationen von komplizierteren und nicht-linearen Funktionen zu verwenden, und bieten eine effizientere Methode zur "Anpassung aller Parameter", die beteiligt sind. Aber im Grunde ist es die gleiche Idee. Hier sind zum Beispiel einige Annäherungen an die "Daten", die in Form von einfacheren mathematischen Funktionen konstruiert wurden:

Ein Vorteil dieser Methode liegt in ihrer Einfachheit: Die Beschaffenheit jedes Modells lässt sich direkt durch seine Formel darstellen. Doch ebenso wie bei den neuronalen Netzen stoßen wir auf Herausforderungen in der Vorhersagegenauigkeit. (Übrigens gibt es eine ganze Reihe von Methoden für Dinge wie Zeitreihenprognose, die Ideen wie "Anpassung an Rekurrenzrelationen“ enthalten – und in der modernen Zeit die Verwendung von Transformer-Neuronalen-Netzen. Und obwohl einige dieser Methoden in der Lage sind, ein periodisches Signal wie eine Sinuswelle gut zu erfassen, erwartet man nicht, dass sie breit gefächert erfolgreich sind, Funktionen genau vorherzusagen.)

Man könnte argumentieren, dass der Ansatz, neuronale Netze auf eine zu spezifische Weise einzusetzen und zu schulen, möglicherweise limitierend wirkt. Die breite und umfassende Datenbasis, auf der beispielsweise ChatGPT trainiert wurde, ist womöglich entscheidend für dessen Fähigkeit, "allgemeine Sprachmuster und Konzepte des gesunden Menschenverstands" zu erlernen – ein Fortschritt, der bei einer Beschränkung auf enger gefasste Datensätze womöglich ausgeblieben wäre.

Was bedeutet das also für uns hier? Es könnte sein, dass wir wollen, dass unser neuronales Netz eine "allgemeine Vorstellung davon hat, wie Funktionen funktionieren" - zum Beispiel, dass es Dinge wie die Kontinuität von Funktionen oder, was das betrifft, Periodizität oder Symmetrie kennt. Wir können also nicht nur auf ein bestimmtes "Fenster" von Daten trainieren, wie wir es oben getan haben, sondern auf ganze Familien von Funktionen, wie Sammlungen trigonometrischer Funktionen oder vielleicht alle eingebauten mathematischen Funktionen in der Wolfram Language.

Und wenn wir das tun, können wir natürlich unsere Sinuskurve erfolgreich vorhersagen – genauso wie wir es tun würden, wenn wir die traditionelle Fourier-Analyse mit Sinuskurven als Grundlage verwenden würden. Aber betreibt man so Wissenschaft?

Im Wesentlichen heißt es: "Ich habe so etwas schon einmal gesehen, also gehe ich davon aus, dass es jetzt so abläuft". Und das kann zweifellos nützlich sein, denn es handelt sich um eine automatisierte Version eines typischen Vorgangs, den ein Mensch mit Erfahrung auf einem bestimmten Gebiet durchführen kann. Wir werden später darauf zurückkommen. Der wichtigste Punkt ist jedoch, dass zumindest bei der Vorhersage von Funktionen neuronale Netze und die heutige KI nicht in der Lage zu sein scheinen, darüber hinauszusehen, was in ihre Konstruktion und ihr Training einfließt. Es gibt keine "emergente Wissenschaft", sondern nur einen ziemlich direkten "Musterabgleich".

Vorhersage von Berechnungsprozessen

Die Vorhersage einer Funktion ist eine besonders schwierige Aufgabe, und man könnte sich vorstellen, dass "reale Prozesse" – etwa in der Natur – mehr "Umgebungsstruktur" haben, die eine KI nutzen könnte, um bei der Vorhersage "Fuß zu fassen". Und als Beispiel für das, was wir als "künstliche Natur" bezeichnen könnten, können wir rechnerische Systeme wie zelluläre Automaten betrachten. Hier ist ein Beispiel dafür, was eine bestimmte Regel eines zellulären Automaten bei einer bestimmten Ausgangsbedingung bewirkt:

Hier gibt es eine Mischung aus Einfachheit und Komplexität. Und als Menschen können wir leicht vorhersagen, was in den einfachen Teilen passieren wird, aber im Grunde können wir nicht viel über die anderen Teile sagen. Wie würde also eine KI vorgehen?

Wenn unsere "KI" einfach nur die Regel des zellulären Automaten ausführen kann, wird sie in der Lage sein, alles vorherzusagen, wenn auch mit großem Rechenaufwand. Die eigentliche Frage ist jedoch, ob eine KI die Dinge abkürzen kann, um erfolgreiche Vorhersagen zu machen, ohne den ganzen Rechenaufwand zu betreiben – oder, anders ausgedrückt, ob die KI erfolgreich Taschen mit reduziertem Rechenaufwand finden und nutzen kann.

Als konkretes Experiment habe ich ein neuronales Netz eingerichtet, um zu versuchen, das Verhalten unseres zellulären Automaten effizient vorherzusagen. Das Netz ist im Grunde ein einfacher – wenn auch "moderner" – Faltungs-Autoencoder mit 59 Schichten und insgesamt etwa 800.000 Parametern:

Es wird ähnlich wie ein LLM trainiert. Wir haben viele Beispiele für die Entwicklung unseres zellulären Automaten erhalten, dann haben wir dem Netzwerk die "obere Hälfte" eines jeden Beispiels gezeigt und versucht, es dazu zu bringen, diese erfolgreich fortzusetzen, um die "untere Hälfte" vorherzusagen. In dem speziellen Experiment, das wir durchgeführt haben, haben wir 32 Millionen Beispiele für die Entwicklung eines zellulären Automaten mit 64 Zellen gegeben. (Und ja, diese Anzahl von Beispielen ist winzig im Vergleich zu allen 2⁶⁴ ≈ 10¹⁹ möglichen Ausgangskonfigurationen). Dann versuchten wir, die Evolution des zellulären Automaten in Abschnitten von 64 Zellen und 64 Schritten einzugeben, und untersuchten, welche Wahrscheinlichkeiten das Netzwerk den verschiedenen möglichen Fortsetzungen zuordnete.

Hier sind einige Ergebnisse für eine Abfolge von verschiedenen Ausgangsbedingungen:

Man sieht das erwartbare: Wenn das Verhalten einfach genug ist, bekommt das Netz es im Grunde richtig hin. Aber wenn das Verhalten komplizierter ist, kommt das Netz in der Regel nicht so gut damit zurecht. Oft ist es zumindest "vage richtig", aber die Details sind nicht vorhanden.

Vielleicht, so könnte man meinen, wurde das Netz einfach nicht lange genug oder nicht mit genügend Beispielen trainiert. Und um ein Gefühl für die Wirkung von mehr Training zu bekommen, sehen Sie hier, wie sich die vorhergesagten Wahrscheinlichkeiten mit einer Viertelmillion aufeinander folgender Trainingsrunden entwickeln:

Und ja, mit mehr Training gibt es eine Verbesserung, aber am Ende scheint es nicht viel besser zu werden. (Allerdings zeigt die Verlustkurve im Laufe des Trainings einige plötzliche Sprünge nach unten, vermutlich weil "Entdeckungen" gemacht werden - und man kann nicht sicher sein, dass es nicht noch mehr davon geben wird.)

Es ist äußerst typisch für das maschinelle Lernen, dass es eine gute Arbeit leistet, wenn es darum geht, Dinge "ungefähr richtig" zu machen. Aber die Details sind nicht das, was maschinelles Lernen in der Regel gut kann. Wenn also das, was man zu tun versucht, davon abhängt, ist das maschinelle Lernen eingeschränkt. Und bei der hier betrachteten Vorhersage besteht das Problem darin, dass, sobald die Dinge auch nur geringfügig aus dem Ruder laufen, alles von da an nur noch schlimmer wird.

Ermittlung der rechnerischen Reduzibilität

Rechnerische Reduzibilität steht im Zentrum dessen, was normalerweise als "Wissenschaft betreiben" verstanden wird. Denn sie ist nicht nur dafür verantwortlich, dass Vorhersagen getroffen werden können, sondern ermöglicht auch die Identifizierung von Regelmäßigkeiten, die Erstellung von Modellen und komprimierten Zusammenfassungen dessen, was gesehen wird – und die Entwicklung eines Verständnisses, das in den Köpfen erfasst werden kann.

Die Frage, wie rechnerische Reduzibilität gefunden werden kann, stellt sich oft. Manchmal ist sie sehr offensichtlich, wie zum Beispiel, wenn eine Visualisierung eines bestimmten Verhaltens (wie die Evolution eines zellulären Automaten) erstellt und sofort einfache Merkmale darin erkannt werden. Doch in der Praxis mag rechnerische Reduzibilität nicht immer so offensichtlich sein, und es könnte erforderlich sein, viele Details zu durchforsten, um sie zu entdecken. Hier kann Künstliche Intelligenz potenziell sehr hilfreich sein.

Auf einer gewissen Ebene kann dies als eine Geschichte von "der Suche nach der richtigen Parametrisierung" oder dem "richtigen Koordinatensystem" betrachtet werden. Als sehr direktes Beispiel kann man diese scheinbar recht zufällige Punktwolke betrachten. Dreht man sie in den entsprechenden Winkel, lassen sich jedoch deutliche Regelmäßigkeiten erkennen:

Gibt es eine allgemeine Methode, um Regelmäßigkeiten zu erkennen, wenn sie vorhanden sind? Die traditionelle Statistik ("Gibt es eine Korrelation zwischen A und B?", und so weiter), die Modellanpassung ("Ist dies eine Summe von Gaußschen Kurven?") und die traditionelle Datenkomprimierung ("Wird es nach der Lauflängenkodierung kürzer?") erkennen nur ganz spezifische Arten von Regelmäßigkeiten. Kann Künstliche Intelligenz also mehr erreichen? Bietet sie vielleicht einen allgemeinen Weg zum Auffinden von Regelmäßigkeiten?

Die Feststellung, eine Regelmäßigkeit in etwas gefunden zu haben, bedeutet im Grunde, dass nicht alle Details der Sache angegeben werden müssen: Es gibt eine reduzierte Darstellung, aus der sie rekonstruiert werden kann. So muss beispielsweise bei der Regelmäßigkeit "Punkte-auf-Linien" im Bild nicht die Position jedes einzelnen Punktes angegeben werden; es genügt zu wissen, dass sie Streifen mit einem bestimmten Abstand bilden.

Angenommen, es gibt ein Bild mit einer bestimmten Anzahl von Pixeln. Es stellt sich die Frage, ob es eine reduzierte Darstellung mit weniger Daten gibt, aus der das Bild effektiv rekonstruiert werden kann. Bei neuronalen Netzen existiert ein Ansatz, um solch eine reduzierte Darstellung zu finden.

Die Grundidee besteht darin, ein neuronales Netz als Autoencoder zu nutzen, der Eingaben entgegennimmt und sie als Ausgaben wiedergibt. Dies mag zunächst wie eine triviale Aufgabe erscheinen. Doch ist sie es nicht, denn die Eingabedaten müssen durch das Innere des neuronalen Netzes fließen, wobei sie anfangs "zermahlen" und am Ende "zusammengesetzt" werden. Der Schlüssel liegt jedoch darin, das neuronale Netz mit ausreichend Beispielen so zu trainieren, dass es die Eingaben erfolgreich wiedergibt und als Autoencoder fungiert.

Der nächste Schritt besteht darin, den Autoencoder zu untersuchen und die reduzierte Darstellung herauszufiltern, die er kreiert hat. Während die Daten im neuronalen Netz von einer Schicht zur nächsten fließen, strebt es danach, die Informationen zu bewahren, die benötigt werden, um die ursprüngliche Eingabe zu reproduzieren. Wenn eine Schicht weniger Elemente enthält, muss das, was in dieser Schicht vorhanden ist, einer reduzierten Darstellung der ursprünglichen Eingabe entsprechen.

Wenn man von einem modernen Standard-Bild-Autoencoder ausgeht, der auf ein paar Milliarden typischerweise im Internet gefundenen Bilder trainiert wurde, und ihm ein Bild einer Katze gibt, wird er erfolgreich etwas reproduzieren, das dem Originalbild ähnelt. Aber in der Mitte wird es eine reduzierte Darstellung mit viel weniger Pixeln geben, die aber immer noch das einfängt, was von der Katze benötigt wird (wie unten dargestellt, mit ihren vier getrennten Farbkanälen):

Dies lässt sich als eine Art "Black-Box-Modell" für das Katzenbild betrachten. Es ist nicht bekannt, was die Elemente ("Merkmale") im Modell bedeuten, aber irgendwie gelingt es, "das Wesen des Bildes" erfolgreich einzufangen. Was passiert also, wenn dies auf "wissenschaftliche Daten" oder zum Beispiel auf "künstliche natürliche Prozesse" wie zelluläre Automaten angewendet wird? Hier zeigt sich ein Fall, in dem eine erfolgreiche Komprimierung erreicht wird. Das oberste Beispiel klappt gut, danach wird es schlimmer, vor allem bei rechnerischer Irreduzibilität:

Aber die Geschichte reicht noch weiter. Der Autoencoder, der zum Einsatz kam, wurde auf "alltägliche Bilder" trainiert, nicht auf solche "wissenschaftlichen Bilder". Er versucht also, die wissenschaftlichen Bilder nach Mustern wie Augen und Ohren zu modellieren, wie sie beispielsweise in Bildern von Katzen vorkommen. Was geschieht nun, wenn ein Autoencoder trainiert wird, der spezifischer auf die Art von Bildern ausgerichtet ist, die benötigt werden – wie im Fall der Vorhersage durch zelluläre Automaten oben beschrieben?

Es gibt zwei sehr einfache neuronale Netzwerke, die als "Encoder" und "Decoder" dienen können, um einen Autoencoder zu konstruieren:

Nun nimmt man den Standard-MNIST-Bilddatensatz und verwendet diesen, um den Autoencoder zu trainieren:

Jedes dieser Bilder hat 28 × 28 Pixel. Aber in der Mitte des Autoencoders befindet sich eine Schicht mit nur zwei Elementen. Das bedeutet also, dass alles, was zur Kodierung aufgefordert wird, auf lediglich zwei Zahlen reduziert werden muss:

Was man hier sieht, ist dass der Autoencoder für Bilder, die mehr oder weniger den trainierten ähneln, es schafft etwas zu rekonstruieren, das zumindest grob richtig aussieht, auch bei starker Komprimierung. Gibt man ihm jedoch andere Bildtypen, ist er nicht so erfolgreich. Er besteht dann darauf, sie so wiederherzustellen, dass sie wie Bilder aus seinem Trainingsset aussehen.

Was passiert nun, wenn man es mit Bildern zellulärer Automaten trainiert? Nehmen Sie 10 Millionen Bilder, die mit einer bestimmten Regel generiert wurden und trainieren damit den Autoencoder. Anschließend füttert man ihn mit ähnlichen Bildern:

Die Ergebnisse sind bestenfalls sehr grob; dieses kleine neuronale Netz konnte die "detaillierten Eigenheiten dieses speziellen zellulären Automaten" nicht erlernen. Wäre es gelungen, die gesamte scheinbare Komplexität der Evolution des zellulären Automaten mit nur zwei Zahlen zu charakterisieren, hätte man dies als beeindruckende wissenschaftliche Leistung betrachten können. Doch wie erwartet, wurde das neuronale Netz durch die rechnerische Irreduzibilität effektiv blockiert.

Aber auch wenn es die "rechnerische Irreduzibilität" nicht ernsthaft durchbrechen kann, ist das neuronale Netz dennoch in der Lage, "nützliche Entdeckungen" zu machen, indem es kleine Stücke rechnerischer Reduzierbarkeit und kleine Regelmäßigkeiten findet. Wenn man etwa Bilder von "rauschenden Buchstaben" nimmt und ein neuronales Netz verwendet, um sie auf Zahlenpaare zu reduzieren und diese Zahlen verwendet, um die Bilder zu positionieren, erhält man einen "dimensional reduzierten Merkmalsraum-Plot", der Bilder verschiedener Buchstaben trennt:

Betrachten Sie etwa eine Sammlung zellulärer Automaten mit verschiedenen Regeln. Ein typisches neuronales Netz würde die Bilder wie unten dargestellt im Merkmalsraum anordnen:

Und ja, es ist fast gelungen, automatisch die vier Verhaltensklassen zu entdecken, die ich Anfang 1983 identifiziert hatte. Aber es ist nicht ganz vollständig. Obwohl dies in gewisser Weise ein schwieriger Fall ist, der direkt mit rechnerischer Irreduzibilität konfrontiert ist. Und es gibt viele Fälle (denken Sie an: Anordnung des Periodensystems basierend auf den Eigenschaften der Elemente; Ähnlichkeit von Flüssigkeitsströmungen basierend auf der Reynolds-Zahl; usw.), bei denen man erwarten kann, dass ein neuronales Netz in Bereiche rechnerischer Reduzibilität vordringt und zumindest vorhandene wissenschaftliche Entdeckungen erfolgreich rekapituliert.

KI in der nicht-menschlichen Welt

Im ursprünglichen Konzept ging es bei KI darum, künstliche Analoga menschlicher Intelligenz zu entwickeln. Und tatsächlich sind die jüngsten großen Erfolge der KI – etwa in der visuellen Objekterkennung oder Sprachgenerierung – alle darauf ausgerichtet, künstliche Systeme zu haben, die das Wesen dessen reproduzieren, was Menschen tun. Es geht nicht darum, dass es eine präzise theoretische Definition gibt, was ein Bild zu einem Bild einer Katze im Gegensatz zu einem Hund macht. Wichtig ist, dass ein neuronales Netz zu den gleichen Schlussfolgerungen kommen kann wie Menschen.

Warum funktioniert das? Wahrscheinlich, weil neuronale Netze das Wesen echter Gehirne erfassen. Natürlich sind künstliche neuronale Netze im Detail nicht identisch mit biologischen Gehirnen. Aber in gewisser Weise ist die große Überraschung der modernen KI, dass es offenbar genug Universalität gibt, um künstliche neuronale Netze funktionell ähnlich wie menschliche Gehirne agieren zu lassen, zumindest wenn es um Dinge wie visuelle Objekterkennung oder Sprachgenerierung geht.

Aber was ist mit Fragen in der Wissenschaft? Auf einer Ebene können wir fragen, ob neuronale Netze das nachahmen können, was menschliche Wissenschaftler tun. Es gibt aber auch eine andere Ebene: Ist es möglich, dass neuronale Netze direkt herausfinden können, wie Systeme – sagen wir in der Natur – sich verhalten? Stellen Sie sich vor, wir studieren einen physikalischen Prozess. Menschliche Wissenschaftler könnten eine menschliche Beschreibung des Systems finden, etwa in Form mathematischer Gleichungen. Aber das System selbst tut einfach direkt, was es tut. Und die Frage ist, ob das etwas ist, was ein neuronales Netz erfassen kann.

Grenzen neuronaler Netze bei der Erkennung von Naturprozessen

Und wenn neuronale Netze nur bei "menschlichen Aufgaben" funktionieren, weil sie architektonisch ähnlich zu Gehirnen sind, gibt es keinen unmittelbaren Grund zu der Annahme, dass sie "rohe natürliche Prozesse" erfassen können, die nichts mit Gehirnen zu tun haben. Was passiert also, wenn KI etwas wie die Vorhersage der Protein-Faltung macht?

Ein Grund dafür dürfte sein, dass, selbst wenn der Prozess des Protein-Faltens nichts mit Menschen zu tun hat, unsere Betrachtung, welche Aspekte wichtig sind, menschlich geprägt ist. Es geht nicht darum, dass ein neuronales Netz die genaue Position jedes Atoms vorhersagen soll – was ohnehin in der Natur selten festgelegt ist. Stattdessen interessiert uns eher, ob das Protein die richtige Grundform und erkennbare Merkmale wie Alpha-Helices hat, sowie ob es funktioniert, wie es soll. Diese Fragen ähneln der Art, wie wir entscheiden, ob ein Bild eine Katze oder einen Hund zeigt – sie liegen im Auge des Betrachters. Wenn ein neuronales Netz also vorhersagen kann, wie sich ein Protein faltet, könnte das teilweise daran liegen, dass es die von Menschen subjektiv gesetzten Kriterien erfüllt, dank seiner dem menschlichen Gehirn ähnlichen Struktur.

Es ist ein wenig wie die Erzeugung eines Bildes mit generativer KI. Auf der Ebene der grundlegenden menschlichen visuellen Wahrnehmung mag es wie etwas aussehen, das wir erkennen. Aber wenn wir es genau betrachten, sehen wir, dass es nicht "objektiv" das ist, was wir denken.

Es war mit der Physik der ersten Prinzipien nie wirklich praktikabel herauszufinden, wie Proteine sich falten. Daher ist es beeindruckend, dass neuronale Netze auch nur annähernd korrekte Antworten liefern können. Wie machen sie das? Ein bedeutender Teil davon ist sicher effektiv das Zuordnen von Proteinsegmenten zu dem, was im Trainingssatz vorhanden ist, und dann "plausible" Wege zu finden, diese Segmente zusammenzufügen. Aber es gibt wahrscheinlich noch etwas anderes. Man kennt bestimmte "Regelmäßigkeiten" in Proteinen (wie Alpha-Helices und Beta-Faltblätter). Es scheint jedoch wahrscheinlich, dass neuronale Netze sich in andere Arten von Regelmäßigkeiten einklinken; sie haben irgendwie Taschen der Irreduzibilität gefunden, von denen nicht bekannt war, dass sie existieren. Und besonders wenn nur ein paar Taschen der Irreduzibilität immer wieder auftauchen, repräsentieren sie effektiv neue, allgemeine "Ergebnisse in der Wissenschaft" (etwa eine neue Art von häufig vorkommendem "Meta-Motiv" in der Proteinstruktur).

Obwohl es grundsätzlich unvermeidlich ist, dass es am Ende eine unendliche Anzahl von Taschen der rechnerischen Irreduzibilität geben muss, ist es zunächst nicht klar, wie bedeutend diese in den Dingen sein könnten, die von Interesse sind, oder wie erfolgreich Methoden neuronaler Netze bei deren Auffindung sein könnten. Man könnte sich vorstellen, dass neuronale Netze, insofern sie die wesentliche Arbeitsweise unseres Gehirns spiegeln, nur in Fällen Taschen der Irreduzibilität finden könnten, in denen auch Menschen sie leicht entdecken könnten, etwa durch Betrachten einer Visualisierung.

Ein wichtiger Punkt ist jedoch, dass das menschliche Gehirn normalerweise nur mit Daten "trainiert" wird, die leicht mit unseren Sinnen erfahren werden: Es wurden das Äquivalent von Milliarden von Bildern gesehen und Zillionen von Klängen gehört. Aber es besteht keine direkte Erfahrung mit den mikroskopischen Bewegungen von Molekülen oder mit einer Vielzahl von Arten von Daten, die wissenschaftliche Beobachtungen und Messgeräte liefern können.

Ein neuronales Netzwerk kann jedoch mit sehr unterschiedlichen "Sinneserfahrungen" aufwachsen – sagen wir, es erlebt direkt den "chemischen Raum" oder auch den "metamathematischen Raum", den Raum finanzieller Transaktionen oder Interaktionen zwischen biologischen Organismen oder was auch immer. Aber welche Arten von Bereichen rechnerischer Reduzierbarkeit gibt es in solchen Fällen? Meistens wissen wir das nicht. Wir kennen die, die der "bekannten Wissenschaft“ entsprechen. Aber auch wenn wir erwarten können, dass andere existieren müssen, kennen wir sie normalerweise nicht.

Werden sie für neuronale Netze "zugänglich" sein? Auch das ist unbekannt. Ganz wahrscheinlich, wenn sie zugänglich sind, dann gibt es eine Darstellung – oder Visualisierung – in der die Irreduzibilität für die Betrachtenden "offensichtlich" sein wird. Aber es gibt viele Möglichkeiten, wie dies scheitern könnte. Zum Beispiel könnte die Irreduzibilität "visuell offensichtlich" sein, aber nur in 3D-Volumen, wo es etwa schwer ist, unterschiedliche Strukturen zu unterscheiden. Oder vielleicht könnte die Irreduzibilität nur durch eine Berechnung offenbart werden, die von einem neuronalen Netz nicht leicht gehandhabt wird.

Unweigerlich gibt es viele Systeme, die rechnerische Irreduzibilität zeigen, und die – zumindest in ihrer vollen Form – für jede "Abkürzungsmethode", basierend auf neuronalen Netzen oder anders, unzugänglich sein müssen. Aber die Frage ist, ob, wenn es eine Tasche der rechnerischen Irreduzibilität gibt, sie von einem neuronalen Netz erfasst werden kann.

Aber einmal mehr steht man vor der Tatsache, dass es keine "modelllosen Modelle" gibt. Ein bestimmter Typ eines neuronalen Netzes wird in der Lage sein, bestimmte Arten der rechnerischen Irreduzibilität leicht zu erfassen; ein anderer wird andere Arten leicht erfassen können. Und ja, es ist immer möglich, ein neuronales Netz zu konstruieren, das jede gegebene spezifische Funktion annähern kann. Aber bei der Erfassung einer allgemeinen Art von rechnerischer Irreduzibilität wird viel mehr verlangt – und was erreicht werden kann, hängt unweigerlich von der zugrundeliegenden Struktur des neuronalen Netzes ab.

Angenommen, ein neuronales Netz kann in einem bestimmten Bereich Vorhersagen treffen. Heißt das, es kann alles vorhersagen? Meistens nicht. Oft gibt es nur in einem kleinen Teilbereich Vorhersagbarkeit, während es darüber hinaus noch viele unvorhersehbare Elemente gibt.

Tatsächlich scheint das beispielsweise bei der Protein-Faltung zu geschehen. Hier sind einige Beispiele für Proteine mit Strukturen, die als ziemlich einfach wahrgenommen werden – und die Vorhersage des neuronalen Netzes (Gelb) stimmt ziemlich gut mit den Ergebnissen der physischen Experimente (graue Röhren) überein. In der oberen Reihe arbeitet das neuronale Netz gut, bei komplexeren Proteinen (mittlere Reihe) ist die Übereinstimmung nicht mehr so gut. Und wie sieht es mit noch komplexeren Proteinen aus (unten)?

Es ist schwer zu beurteilen, wie gut das neuronale Netz in diesem Fall funktioniert; es scheint wahrscheinlich, dass es, besonders wenn es "Überraschungen" gibt, diese nicht erfolgreich erfassen wird. (Natürlich könnte es sein, dass alle "vernünftigen Proteine", die normalerweise in der Biologie vorkommen, bestimmte Merkmale aufweisen, und es könnte "unfair" sein, das neuronale Netz auf "unbiologische" zufällige Proteine anzuwenden – obwohl zum Beispiel im adaptiven Immunsystem die Biologie tatsächlich zumindest kurze "zufällige Proteine" effektiv generiert.)

Gleichungen lösen mit KI

In der traditionellen mathematischen Wissenschaft ist der typische Aufbau: Hier sind einige Gleichungen für ein System; lösen Sie sie, um herauszufinden, wie sich das System verhält. Vor dem Einsatz von Computern bedeutete dies in der Regel, dass man eine geschlossene Formel für die Lösung finden musste. Aber mit Computern gibt es einen alternativen Ansatz: eine diskrete numerische Annäherung und eine Art schrittweise Lösung der Gleichungen. Um genaue Ergebnisse zu erhalten, sind jedoch viele Schritte und ein hoher Rechenaufwand erforderlich. Die Frage ist also: Kann KI dies beschleunigen? Und kann KI etwa direkt von den Anfangsbedingungen einer Gleichung zu einer vollständigen Lösung übergehen?

Nehmen wir als Beispiel ein klassisches Beispiel aus der mathematischen Physik: das Dreikörperproblem. Welchen Bahnen werden die Massen folgen, wenn die Ausgangspositionen und -geschwindigkeiten von drei Punktmassen gegeben sind, die über ein inverses quadratisches Gravitationsgesetz wechselwirken? Es gibt eine große Vielfalt – und oft auch eine große Komplexität – , weshalb das Dreikörperproblem eine solche Herausforderung darstellt:

Was aber, wenn man in neuronales Netz auf viele Musterlösungen trainiert? Kann es dann die Lösung in einem bestimmten Fall herausfinden? Im Folgenden habe ich ein recht einfaches "mehrschichtiges Perzeptron"-Netz verwendet:

Ich habe das neuronale Netz mit Anfangsbedingungen gefüttert und es gebeten, eine Lösung zu erzeugen. Hier sind einige Beispiele dafür, was es tut, wobei die richtigen Lösungen durch die helleren Hintergrundpfade gekennzeichnet sind:

Wenn die Bahnkurven (Trajektorien) recht einfach sind, schneidet das neuronale Netz recht gut ab. Aber wenn die Dinge komplizierter werden, ist es immer weniger gut. Es ist, als ob sich das neuronale Netz die einfachen Fälle "erfolgreich eingeprägt" hat, aber nicht weiß, was es in komplizierteren Fällen tun soll. Letztlich ähnelt dies dem, was wir oben bei Beispielen wie der Vorhersage der Evolution von Zellularautomaten (und vermutlich auch der Proteinfaltung) gesehen haben.

Und ja, dies ist wieder einmal eine Geschichte der rechnerischen Irreduzibilität. Die Forderung, die Lösung einfach in einem Durchgang zu erhalten, bedeutet, dass man eine vollständige rechnerische Reduzierbarkeit anstrebt. Und insofern man sich vorstellen könnte, dass man – wenn man nur wüsste, wie man es macht – im Prinzip immer eine "geschlossene Formel" für die Lösung erhalten könnte, geht man implizit von rechnerischer Reduzierbarkeit aus. Aber seit vielen Jahrzehnten bin ich der Meinung, dass so etwas wie das Dreikörperproblem in Wirklichkeit ziemlich viel rechnerische Irreduzibilität aufweist.

Wäre ein neuronales Netz in der Lage gewesen, das Problem zu "knacken" und sofort Lösungen zu generieren, hätte das natürlich die rechnerische Reduzierbarkeit bewiesen. So aber ist das offensichtliche Versagen der neuronalen Netze ein weiterer Beweis für die rechnerische Irreduzibilität des Dreikörperproblems. (Es ist übrigens erwähnenswert, dass das Dreikörperproblem zwar eine empfindliche Abhängigkeit von den Anfangsbedingungen aufweist, aber das ist hier nicht das Hauptproblem; vielmehr geht es um die tatsächliche Eigenkomplexität der Trajektorien).

Wir wissen bereits, dass diskrete Rechensysteme wie zelluläre Automaten voller rechnerischer Irreduzibilität sind. Und wir hätten uns vorstellen können, dass kontinuierliche Systeme – die beispielsweise durch Differenzialgleichungen beschrieben werden – mehr Struktur haben, sodass sie die rechnerische Irreduzibilität vermeiden. Und da neuronale Netze (in ihrer üblichen Formulierung) mit kontinuierlichen Zahlen arbeiten, hätte man meinen können, dass sie in der Lage wären, die Struktur kontinuierlicher Systeme zu erfassen, um sie vorhersagen zu können. Aber etwas scheint es so, als ob die "Kraft der rechnerischen Irreduzibilität" zu stark ist und letztlich die Möglichkeiten neuronaler Netze übersteigt.

Dennoch können neuronale Netze bei der Lösung von Gleichungen von großem praktischen Nutzen sein. Herkömmliche numerische Näherungsmethoden neigen dazu, lokal und inkrementell (wenn auch oft adaptiv) zu arbeiten. Neuronale Netze können jedoch leichter mit "viel größeren Fenstern" umgehen, sie kennen gewissermaßen "längere Verhaltensabläufe" und sind in der Lage, über diese hinweg "vorauszuspringen". Außerdem können neuronale Netze bei einer enormen Anzahl von Gleichungen (etwa in der Robotik oder Systemtechnik) in der Regel einfach "alle Gleichungen aufnehmen und etwas Vernünftiges tun", während herkömmliche Methoden die Gleichungen tatsächlich einzeln bearbeiten müssen.

Das Dreikörperproblem beinhaltet gewöhnliche Differenzialgleichungen. Viele praktische Probleme beruhen jedoch auf partiellen Differenzialgleichungen (PDGen), bei denen sich nicht nur einzelne Koordinaten, sondern ganze Funktionen f× usw. mit der Zeit entwickeln. Und ja, auch hier kann man neuronale Netze einsetzen, oft mit erheblichem praktischen Nutzen. Aber was ist mit der rechnerischen Irreduzibilität? Viele der in der Praxis am meisten untersuchten Gleichungen und Situationen (z. B. für technische Zwecke) neigen dazu, sie zu vermeiden, aber im Allgemeinen gibt es sie natürlich (insbesondere bei Phänomenen wie der Turbulenz von Flüssigkeiten). Und wenn es eine rechnerische Irreduzibilität gibt, kann man letztlich nicht erwarten, dass neuronale Netze gut funktionieren. Aber wenn es darum geht, unsere menschlichen Bedürfnisse zu befriedigen - wie in anderen Beispielen, die wir besprochen haben - kann es besser aussehen.

Nehmen wir als Beispiel die Vorhersage des Wetters. Letztlich geht es hier um PDGen für die Strömungsdynamik (und ja, es gibt auch andere Effekte, die mit Wolken usw. zu tun haben). Man kann sich vorstellen, diese PDGen direkt und rechnerisch zu lösen. Ein anderer Ansatz wäre jedoch, ein neuronales Netz einfach "typische Wettermuster lernen" zu lassen (wie es die Meteorologen früherer Zeiten tun mussten), und dann das Netz (ähnlich wie bei der Proteinfaltung) versuchen zu lassen, diese Muster so zusammenzusetzen, dass sie zu jeder Situation passen.

Wie erfolgreich wird das sein? Das hängt wahrscheinlich davon ab, womit wir uns beschäftigen. Es könnte sein, dass ein bestimmter Aspekt des Wetters eine beträchtliche rechnerische Reduzibilität aufweist und recht gut vorhersagbar ist, beispielsweise durch neuronale Netze. Und wenn dies der Aspekt des Wetters ist, der uns interessiert, könnten wir zu dem Schluss kommen, dass das neuronale Netz seine Sache gut macht.

Falls ein für uns wichtiges Thema, wie die Frage "Wird es morgen regnen?", sich nicht einfach durch Berechnungen vorhersagen lässt, können neuronale Netze meist keine zuverlässigen Prognosen liefern. In solchen Fällen müssen wir auf umfangreiche und möglicherweise aufwendige Berechnungen zurückgreifen.

Teil 2 des Beitrags folgt in der kommenden Woche. Ein Hinweis: Wenn Sie im englischsprachigen Originalartikel "Can AI Solve Science?" auf ein beliebiges Diagramm klicken, erhalten Sie den Code in Wolfram Language, um die Ergebnisse zu reproduzieren. Der Code zum Trainieren der verwendeten neuronalen Netze ist ebenfalls verfügbar (setzt eine GPU voraus).

(vza)